Gradiente Descendiente: Una Guía Completa

El gradiente descendiente es una técnica esencial en el mundo del aprendizaje automático y la inteligencia artificial, proporcionando un método para optimizar las funciones de coste y mejorar los modelos predictivos. A lo largo de este artículo, exploraremos los conceptos, las matemáticas y las aplicaciones prácticas del gradiente descendiente en una variedad de contextos.

Contenido

¿Qué es el Gradiente Descendiente?
Importancia en Aprendizaje Automático
Fundamentos Matemáticos del Gradiente Descendiente
Concepto de Derivada
Función de Coste
Minimización de la Función de Coste
Gradiente Descendiente por Lotes
Gradiente Descendiente Estocástico
Gradiente Descendiente Mini-Lote
En Redes Neuronales
En Regresión Lineal
Desafíos y Soluciones en el Uso del Gradiente Descendiente
Herramientas y Tecnologías Relacionadas
TensorFlow
PyTorch
Resumen de Puntos Clave
Preguntas Frecuentes sobre el gradiente descendiente

¿Qué es el Gradiente Descendiente?

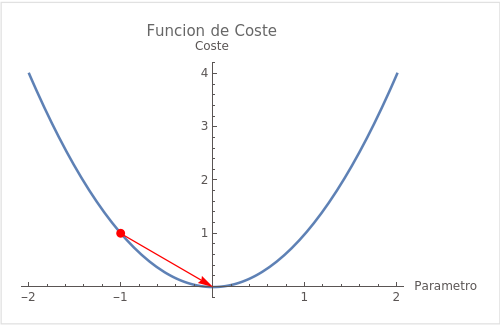
El gradiente descendiente es un algoritmo de optimización que busca encontrar el mínimo local de una función de coste. En el contexto del aprendizaje automático, esta función de coste representa el error o la diferencia entre las predicciones del modelo y los datos reales. El "descenso" se refiere al proceso de moverse hacia abajo en la superficie de la función de coste, ajustando los parámetros del modelo para minimizar el error. Este ajuste se realiza de manera iterativa, paso a paso, mejorando gradualmente la precisión del modelo en sus predicciones.

Importancia en Aprendizaje Automático

El aprendizaje automático se centra en la creación de modelos que pueden aprender de los datos para hacer predicciones o tomar decisiones. El gradiente descendiente juega un papel crucial en este proceso, proporcionando un mecanismo para ajustar los parámetros del modelo, como los pesos en una red neuronal, para mejorar progresivamente su rendimiento. La capacidad de un modelo para aprender y adaptarse a través del gradiente descendiente es fundamental para el desarrollo de sistemas de inteligencia artificial eficientes y efectivos.

Fundamentos Matemáticos del Gradiente Descendiente

Concepto de Derivada

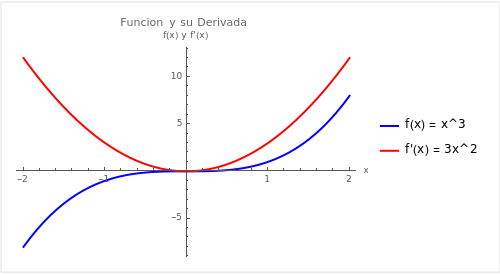
La derivada de una función en un punto dado describe la tasa de cambio de la función en ese punto. En el contexto del gradiente descendiente, utilizamos la derivada para determinar la pendiente de la función de coste en un punto particular y, por lo tanto, para entender en qué dirección debemos ajustar nuestros parámetros para minimizar la función de coste.

Función de Coste

La función de coste, o función de pérdida, cuantifica el error entre las predicciones del modelo y los datos reales. En el aprendizaje supervisado, donde los datos de entrenamiento incluyen la "respuesta correcta", la función de coste puede calcularse como la diferencia entre la predicción del modelo y este valor verdadero.

Minimización de la Función de Coste

El objetivo del gradiente descendiente es minimizar la función de coste ajustando iterativamente los parámetros del modelo. En cada paso, los parámetros se ajustan en la dirección opuesta al gradiente de la función de coste, moviéndose así hacia el mínimo local.

Gradiente Descendiente por Lotes

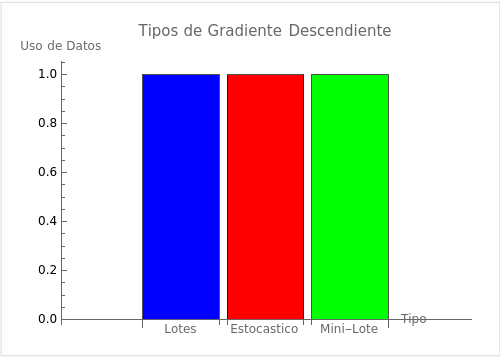
El gradiente descendiente por lotes, o Batch Gradient Descent, utiliza todo el conjunto de datos para calcular el gradiente de la función de coste en cada iteración del entrenamiento. Aunque es computacionalmente costoso y a veces impracticable en conjuntos de datos muy grandes, tiene la ventaja de producir actualizaciones estables y consistentes en los parámetros del modelo.

Gradiente Descendiente Estocástico

A diferencia del método por lotes, el Gradiente Descendiente Estocástico (SGD) actualiza los parámetros del modelo utilizando solo un ejemplo de entrenamiento a la vez. Aunque SGD puede ser más ruidoso y menos preciso en términos de la dirección del gradiente, a menudo llega mucho más rápido a la convergencia debido a la frecuencia de las actualizaciones.

Gradiente Descendiente Mini-Lote

El Gradiente Descendiente Mini-Lote es un término medio entre los dos anteriores. En lugar de utilizar todo el conjunto de datos o un solo ejemplo, SGD mini-lote utiliza un subconjunto aleatorio de los datos en cada iteración. Este método combina la eficiencia computacional de SGD con la estabilidad y precisión del gradiente descendiente por lotes.

En Redes Neuronales

Las redes neuronales utilizan el gradiente descendiente para ajustar los pesos de las conexiones neuronales. A través de múltiples capas y nodos, las redes neuronales pueden aprender patrones complejos y realizar tareas como clasificación de imágenes, reconocimiento de voz y más.

En Regresión Lineal

La regresión lineal es una de las aplicaciones más simples del gradiente descendiente. El algoritmo se utiliza para encontrar la línea que mejor se ajusta a los datos de entrenamiento minimizando la suma de los cuadrados de los residuos (la diferencia entre las predicciones del modelo y los datos reales).

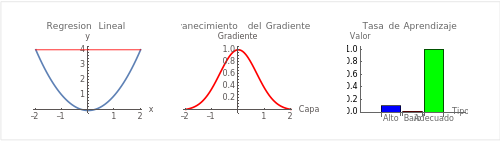
Regresión Lineal: La línea roja representa una línea de regresión que intenta ajustarse a los datos (representados por la parábola).
Desvanecimiento del Gradiente: La gráfica muestra cómo el gradiente (valor de la derivada) puede disminuir a medida que se retropropaga a través de las capas de una red neuronal, lo que es un problema especialmente en redes profundas.
Tasa de Aprendizaje: El gráfico de barras muestra diferentes valores para la tasa de aprendizaje: alto, bajo y adecuado, que pueden afectar la velocidad y la capacidad del algoritmo de gradiente descendiente para converger al mínimo global.

Desafíos y Soluciones en el Uso del Gradiente Descendiente

Problema de Desvanecimiento del Gradiente

El desvanecimiento del gradiente es un problema que ocurre durante el entrenamiento de redes neuronales profundas cuando los gradientes tienden a desvanecerse a medida que la propagación hacia atrás avanza a través de las capas. Este fenómeno puede hacer que el entrenamiento sea extremadamente lento o incluso hacer que la red no pueda aprender adecuadamente. Soluciones como la inicialización de pesos cuidadosa y el uso de funciones de activación, como ReLU, han sido propuestas para mitigar este problema.

Tasa de Aprendizaje

La elección de la tasa de aprendizaje es crucial en el entrenamiento de modelos utilizando gradiente descendiente. Una tasa de aprendizaje demasiado alta puede hacer que el modelo oscile o incluso diverja, mientras que una tasa de aprendizaje demasiado baja puede resultar en una convergencia extremadamente lenta. Métodos como la búsqueda de cuadrícula y técnicas de ajuste adaptativo de la tasa de aprendizaje se utilizan comúnmente para encontrar un valor adecuado.

Herramientas y Tecnologías Relacionadas

TensorFlow

TensorFlow es una biblioteca de código abierto desarrollada por Google que proporciona un conjunto de herramientas completo para trabajar con modelos de aprendizaje automático, incluyendo redes neuronales profundas. TensorFlow ofrece una amplia variedad de funciones y se utiliza tanto en la investigación académica como en la producción a gran escala.

PyTorch

Desarrollado por Facebook, PyTorch es otra biblioteca de aprendizaje profundo que ha ganado popularidad por su flexibilidad y eficiencia, especialmente en la investigación académica. PyTorch proporciona un entorno dinámico y fácil de usar, lo que facilita la experimentación y el prototipado de modelos.

Resumen de Puntos Clave

El gradiente descendiente es un pilar en el aprendizaje automático y la inteligencia artificial, permitiendo que los modelos aprendan y se adapten para mejorar su rendimiento. A través de una comprensión sólida de los fundamentos matemáticos y una aplicación cuidadosa en diferentes tipos y aplicaciones prácticas, los practicantes pueden utilizar el gradiente descendiente para desarrollar modelos robustos y eficientes.

Preguntas Frecuentes sobre el gradiente descendiente

1. ¿Cómo se elige la tasa de aprendizaje en el gradiente descendiente?

La elección de la tasa de aprendizaje es fundamental y puede influir significativamente en el rendimiento del modelo. A menudo, se realiza una búsqueda de cuadrícula o se utilizan métodos de ajuste adaptativo para encontrar una tasa de aprendizaje que permita que el modelo converja de manera eficiente sin oscilar o divergir.

2. ¿Cuáles son las alternativas al gradiente descendiente en la optimización de modelos de aprendizaje automático?

Existen varios algoritmos alternativos para la optimización de modelos, como el Gradiente Conjugado, BFGS, y algoritmos evolutivos, cada uno con sus propias ventajas y desventajas dependiendo del contexto y del tipo de problema que se esté abordando.

3. ¿Cómo afecta la inicialización de los pesos al proceso de entrenamiento en el gradiente descendiente?

La inicialización de los pesos puede influir significativamente en la velocidad de convergencia y en la calidad del modelo final. Inicializaciones pobres pueden llevar a convergencias lentas y mínimos locales subóptimos. Estrategias como la inicialización de He o Xavier son comúnmente utilizadas para establecer los pesos iniciales de manera efectiva.

4. ¿Es el gradiente descendiente aplicable a todos los modelos de aprendizaje automático?

Aunque el gradiente descendiente es ampliamente aplicable, no es adecuado para todos los modelos o problemas. Algunos modelos no tienen una función de coste diferenciable, haciendo que el gradiente descendiente no sea aplicable. En tales casos, se pueden explorar otros métodos de optimización.

5. ¿Cómo se manejan los mínimos locales en el gradiente descendiente?

Los mínimos locales pueden ser un desafío en el gradiente descendiente, especialmente en problemas no convexos. Técnicas como el recocido simulado, el uso de momentum, o algoritmos de optimización estocástica pueden ayudar a evitar que el algoritmo quede atrapado en mínimos locales subóptimos.